Chapter 5 Application of Catalan Numbers

Here we discover some application of catalan numbers in real problem solving. For example, some knowledge content about combinatorial and discrete mathematics.

5.1 Paths on a triangle

Definition 5.1 Let \(\mathcal{T}\subset \mathbb{N}^2\) denote the infinite “triangle” \[ \mathcal{T}=\big\{(k,n),\quad 0\leq k\leq n \big\} \] (see the figure below).

For \((k,n) \in \mathcal{T}\) we denote by \(P_{k,n}\) the number of paths such that: * the path starts at \((0,0)\) ends at \((n,k)\) and entirely lies inside \(\mathcal{T}\) * the paths only takes unit steps in the North and East directions.

For example this figure shows that \(P_{2,3}=5\):

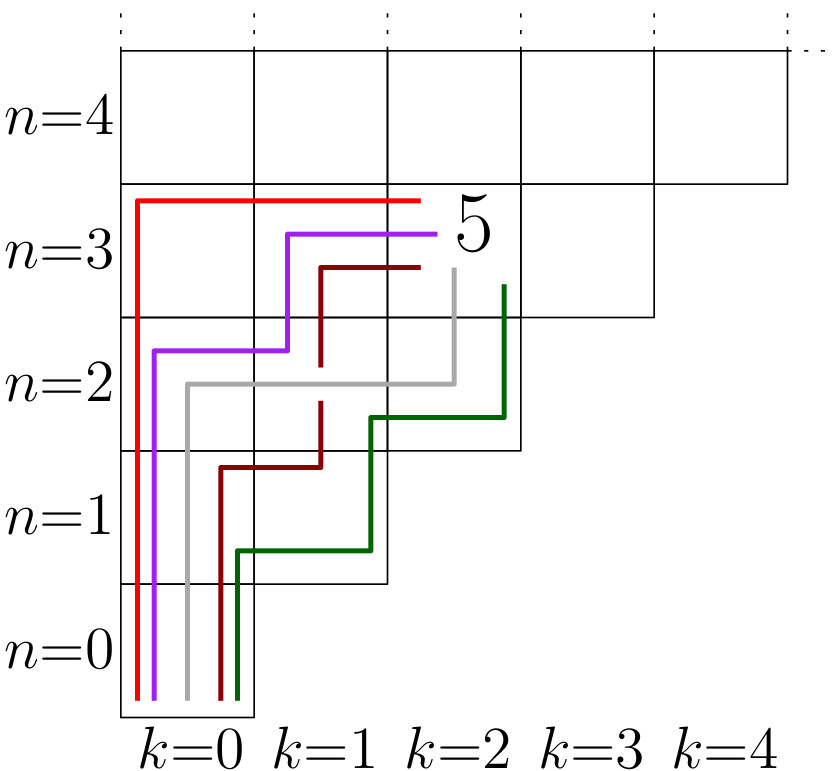
Escalier

Figure 5.1: Escalier

We write a function Paths(K,N) which returns a table (or a matrix) of all the values of \(P_{k,n}\) for \(k\leq K, n\leq N\).

# implement of the function Path
# we use the recursive method by implement the auxiliary function Path
def Path(k, n):
    res = [['']]
    up_count = [[0]]
    right_count = [[0]]
    if n == 0:
        return []
    if k == 0:
        return ['up ' * n]
    for i in range(1, n + k + 1):
        res.append([])
        up_count.append([])
        right_count.append([])
        for j in range(len(res[i-1])):
            curr_path = res[i-1][j]
            if up_count[i-1][j] < n:
                res[i].append(curr_path + 'up ')
                up_count[i].append(up_count[i-1][j] + 1)
                right_count[i].append(right_count[i-1][j])
            if right_count[i-1][j] < k:
                if right_count[i-1][j] < up_count[i-1][j]:
                    res[i].append(curr_path + 'right ')
                    up_count[i].append(up_count[i-1][j])
                    right_count[i].append(right_count[i-1][j] + 1)
    return res[-1]


def Paths(K, N):
    result = np.zeros((K + 1, N + 1))
    for k in range(K + 1):
        for n in range(N + 1):
            result[k, n] = len(Path(k, n))

    return result
    
print("--------- Another Test Sample ----------")
print(Paths(5, 6))
print("--------- Test Sample for Calatan number ----------")
lis = []
matrix = Paths(5, 6)
for i in range(6):
    lis.append(matrix[i][i + 1])
print(lis)

--------- Another Test Sample ----------
[[  0.   1.   1.   1.   1.   1.   1.]
 [  0.   1.   2.   3.   4.   5.   6.]
 [  0.   0.   2.   5.   9.  14.  20.]
 [  0.   0.   0.   5.  14.  28.  48.]
 [  0.   0.   0.   0.  14.  42.  90.]
 [  0.   0.   0.   0.   0.  42. 132.]]
--------- Test Sample for Calatan number ----------
[1.0, 2.0, 5.0, 14.0, 42.0, 132.0]

We denote the sequence \(u_{k}=P_{k, k+1}\). From the matrix we can find that \(u_k\) is same with the sequence of the Calatan Number, which means \(P_{k,k+1}=c_{k}=\sum_{j=0}^{k-1}=c_{k}c_{n-1-k}\). Now lets prove it.

First we try to discuss in a more simple model. For example, I try to compute \(P_{3, 4}=14\). For each points \((k, k+1)\) where \(1 \leq k \leq 3\), we consider those points as step points, which means for example, we consider \((2,3)\) as an intermediate point, we have for all the possible paths to \((3,4)\) go through \((2,3)\), is the multiple of \(P_{2,3} \cdot P_{2,1}=c_{0}c_{2}\). For each step point, the paths go through the step points we can consider the process of two parts, from \((0,0)\) to the step points and from step points to \((k,k+1)\).

Then we can expand this model into more general cases. we try to compute \(P_{k, k+1}\), the for all step points \((m, m+1)\) where \(0 \leq m \leq k-1\). For all the possible paths to \(P_{k, k+1}\), we know it go through at least one step point, since all the paths start from \((0,0)\) and has to go through \((0,1)\) cause we have to go up at the beginning. Therefore we can consider all the paths into to step. First from \((0,0)\) to the step point, which we have \(P_{m,m+1}\) and from the step point to \((k,k+1)\), which is equivalent to from \((0, 1)\) to \((k-m-1,k-m)\), we have \(P_{k-m-1,k-m}\) possibilities. Then number of paths to \((k,k+1)\) is the multiplication of \(P_{m,m+1}\) and \(P_{k-m-1,k-m}\). So we have the sum for all step points that \[ P_{k, k+1} = \sum_{m=0}^{k-1}P_{k-m-1,k-m}P_{m,m+1} \] Since \(P_{0,1}=1\) and \(P_{1,2}=2\). And \(c_{k}=\sum_{j=0}^{k-1}=c_{k}c_{n-1-k}\) by the recursive formula of the Catalan number. Therefore we prove that \[ P_{k,k+1}=c_{k}=\sum_{j=0}^{k-1}=c_{k}c_{n-1-k} \] Also we have \(P_{k,k}\) is also Catalan number, which is easy to explain since \(P_{k,k}=P_{k,k+1}\), since from \((k,k)\) to \((k,k+1)\) there only on way which is go on step on direction East, so we have \[ P_{k,k}=P_{k,k+1}=c_{k}=\sum_{j=0}^{k-1}=c_{k}c_{n-1-k} \] So the paths to diagonal positions are also Catalan numbers.

We can also use other method to prove Path(K,K) is Catalan Numbers.

The method is from (Wiki Page) of Catalan number. We count the number of paths which start and end on the diagonal of a \(n \times n\) grid. All such paths have n right and n up steps. Since we have \(2n\) steps in total, therefore all the possibility are binomial number \(\binom{2n}{n}\).

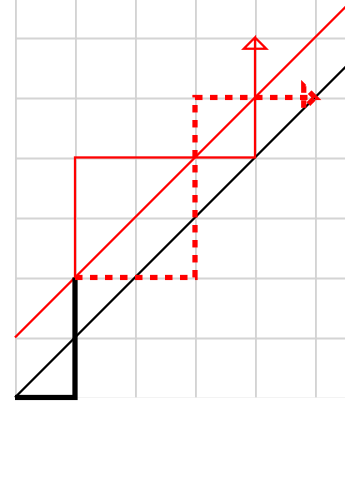
Graph of the algorithms

Figure 5.2: Graph of the algorithms

However, we are restrict by the triangle. As the graph shown above, the path below the diagonal line is not valid. Therefore, we use make the invalid portion of the path flipped like the graph shown. Since we have \(2n\) steps in total and now we have \(n+1\) up then we got \(n-1\) right steps. Due to this reason, we reach at \((n-1, n+1)\) in the end. Because every monotonic path in the \((n - 1) \times (n + 1)\) grid meets the higher diagonal, and because the reflection process is reversible, the reflection is therefore a bijection between bad paths in the original grid. Therefore, for the bad paths we got \[ \left(\begin{array}{c} n-1+n+1 \\ n-1 \end{array}\right)=\left(\begin{array}{c} 2 n \\ n-1 \end{array}\right)=\left(\begin{array}{c} 2 n \\ n+1 \end{array}\right) \] And the valid paths of the Catalan paths are \[ C_n=\left(\begin{array}{c} 2 n \\ n \end{array}\right)-\left(\begin{array}{c} 2 n \\ n+1 \end{array}\right)=\frac{1}{n+1}\left(\begin{array}{c} 2 n \\ n \end{array}\right) \]

5.2 Well-formed parentheses expressions

Definition 5.2 It can be shown that \(c_n\) counts the number of expressions containing \(n\) pairs of parentheses which are correctly matched. For the first values we obtain \[ \begin{array}{r c c c c c} n=1: & () & & & & \\ n=2: & (()) & ()() & & & \\ n=3: & ((())) & (())() & ()(()) & ()()() & (()()) \\ \end{array} \]

Write a recursive function Parentheses(n) which returns the list of all well-formed parentheses expressions with \(n\) pairs of parentheses and check for different values that the list has length \(c_n\)

As we mentioned above, the Well-formed parentheses expressions Parentheses(k) is exactly the same in the Paths on triangle problem from \((0,0)\) to \((k,k)\), Paths(k,k).

We can consider ( as a step in the North direction and ) as a step in the East direction. For every well-formed parentheses expression, we start from (, and the condition for an well-formed parentheses is at any point, the number of ( is larger than ). For example, ()((())), we can see that at any index of this expression, the number of ( before the index is larger than ). These conditions correspond to the condition in the Paths on triangle model that the first step we go up, and the steps in the North direction is always larger than the steps in the East direction otherwise we are out of the triangle board. From \((0,0)\) to \((k,k)\), we has the same number of steps in the North and East direction which is the same that we have same amount of ( and ). Therefore we prove that Parentheses(k) is counted by Catalan numbers.

Or we explain in this way. We have \(p(0) = 1\) as there is only one way to arrange no parentheses and \(p(1)= 1\).

For \(n \geq 2\), we can consider the well-formed parentheses expression as two part, (part1)part2 where part 1 and part 2 are splited by a pair of racket. Then we assume part 1 has \(k\) paris of parentheses and part 2 has \(n-1-k\) paris of parentheses. Since \(k \in [0, n-1]\). Therefore we have the expression \[ p_{n}=\mathcal\sum_{k=0}^{n-1} p_{k}p_{n-1-k} \] This agrees with the formula of the catalan number.

5.3 Binary trees

A binary tree is a tree in which every internal node (in grey in above pictures) has exactly two children. Leaves (in green) have no children. The size of a binary tree is its number of internal nodes. There is one binary tree of size \(1\), and two binary trees of size \(2\), five binary trees of size 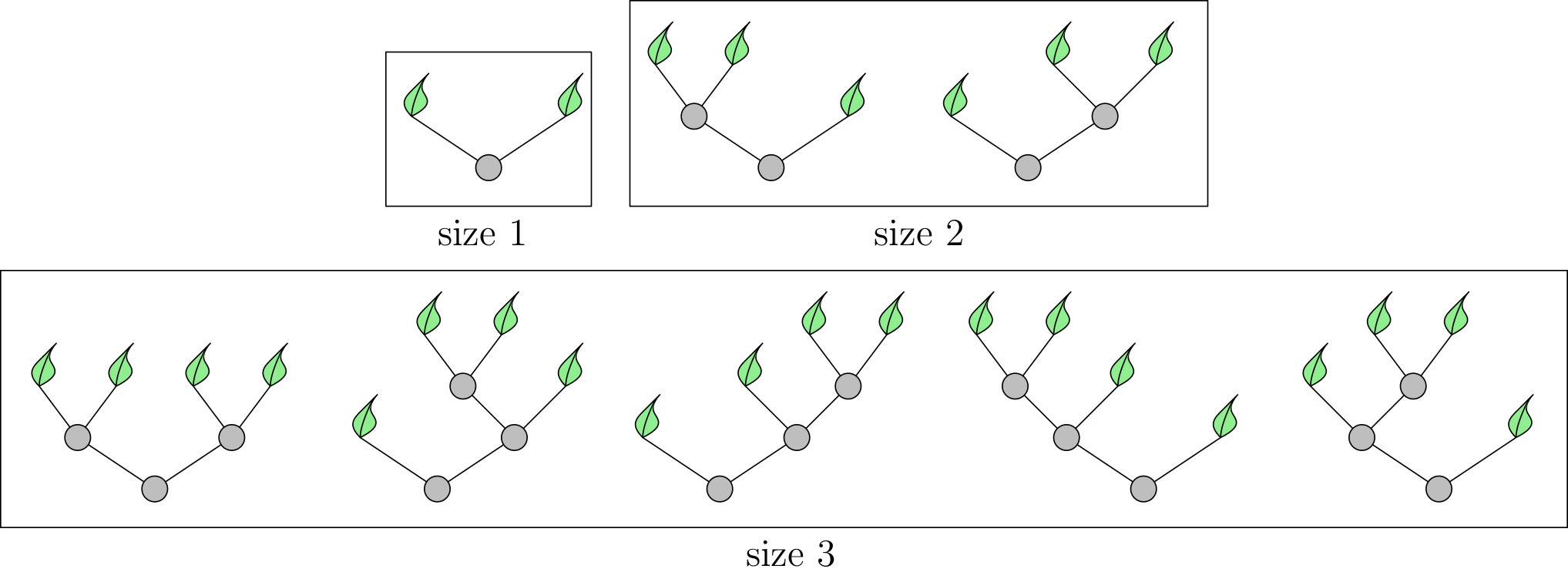\(3\):
Binary Tree

Figure 5.3: Binary Tree

Let \(t_n\) be the number of binary trees of size \(n\), by convention we put \(t_0=1\) (this corresponds to a leaf without any internal node).

We can prove that \(t_n\) is the \(n\)-th Catalan number.

For the Catalan numbers, we have the definition that \[\begin{align*} c_0&=1\\ c_1&=1\\ c_n&=\sum_{k=0}^{n-1} c_kc_{n-1-k}=c_0c_{n-1}+c_1c_{n-2}+\dots +c_{n-1}c_0 \qquad (\text{ for }n\geq 2). \end{align*}\]

Which can also be rewritten as: \[\begin{align*} c_0&=1\\ c_1&=1\\ c_{n+1}&=\sum_{k=0}^{n} c_kc_{n-k} \end{align*}\]

For \(t_1 = 1\) we have zero parent so there only one case. Then we consider more general cases for \(n \geq 2\). We imagine a tree \(t\) with \(n+1\) nodes has one root with two subtrees as children \(t_1\) and \(t_2\). Since the root of \(t\) is a parent node, \(t_1\) and \(t_2\) must have \(n\) parent nodes together (i.e the sum of nodes for \(t_1\) and \(t_2\) is n). A subtree \(t_1\) or \(t_2\) can be empty. Therefore the ways of organize \(t_1\) which k nodes is \(T_{k} T_{n-k}\). Then we have \[ \sum_{i=0}^n T_i T_{n-i} \] Since \(i \in [0,n]\). So we finish the prove that the \(n\)-th Catalan number.