Chapter 4 Dealing with Large Catalan Numbers

In this part, we will explore some of the properties of large catalan numbers.

4.1 Catalan and modulos: the Bostan Conjecture

Information 4.1
Alin Bostan (computer scientist at INRIA and Ecole Polytechnique) conjectured a few years ago (see this link p.26) that in basis 10 the last digit of $c_{n}$ is never $3$ . So far this is still an open problem.

Check the conjecture for $1 \leq n \leq 100$ . The output should look like

Catalan 1 mod 10 is 1: the Conjecture is True
Catalan 2 mod 10 is 2: the Conjecture is True
Catalan 3 mod 10 is 5: the Conjecture is True
Catalan 4 mod 10 is 4: the Conjecture is True
...

# We test the conjecture for 1 to 100
for n in range(1, 101):
    if CatalanClosedForm(n) % 10 != 3:
        print('Catalan', n, 'mode 10 is',
              CatalanClosedForm(n) % 10, ':the Conjecture is', True)
    else:
        print('the Conjecture is', False)
        
Catalan 10 mode 10 is 6 :the Conjecture is True
Catalan 11 mode 10 is 6 :the Conjecture is True
Catalan 12 mode 10 is 2 :the Conjecture is True
Catalan 13 mode 10 is 0 :the Conjecture is True
...
Catalan 99 mode 10 is 8 :the Conjecture is True
Catalan 100 mode 10 is 2 :the Conjecture is True

How to check the conjecture for very large values? Try for example with $7000 \leq n \leq 7100$ .

def precalc(MOD, num):
    catalan = [0] * num
    catalan[0], catalan[1] = 1, 1
    for i in range(2, num):
        total = 0
        for j in range(1, i+1):
            left = catalan[j-1] % MOD
            right = catalan[i-j] % MOD
            total = (total + (left * right) % MOD) % MOD
        catalan[i] = total
    return catalan


if __name__ == '__main__':
    catalan = precalc(10, 8000)
    for i in range(7000, 7101):
        if catalan[i] != 3:
            print('Catalan', i, 'mode 10 is', catalan[i], ':the Conjecture is',
                  True)
        else:
            print('the Conjecture is', False)
            
Catalan 7000 mode 10 is 4 :the Conjecture is True
Catalan 7001 mode 10 is 4 :the Conjecture is True
Catalan 7002 mode 10 is 8 :the Conjecture is True
...
Catalan 7099 mode 10 is 0 :the Conjecture is True
Catalan 7100 mode 10 is 0 :the Conjecture is True

Since our previous function is not that efficient, we need to apply other algorithms. We use the property that $(a \cdot b) mod p = ((a mod p) \cdot (b mod p)) mod p$ This is easy to prove, we assume that $k_{1} = (a mod p)$ and $k_{2} = (b mod p))$ . Therefore, we have $a = m q + k_{1}$ and $b = n q + k_{2}$ where $m, n \in Z$ . We have $\begin{aligned} (a \cdot b) mod p & = (m n q^{2} + (m k_{2} + n k_{1}) q + k_{1} k_{2}) mod p \\ = (k_{1} k_{2}) mod p \\ = ((a mod p) \cdot (b mod p)) mod p \end{aligned}$ Then we can use this property to write the recursive function as above. After all the computation, we find that the conjecture is true for $0 \leq n \leq 7101$ .

More generally, what is the frequency of $0, 1, \dots, 9$ among last digits of the $n$ first Catalan numbers?

# we use a dictionary to store the frequency of the last digit of Catalan numbers
# we test the case with n = 1000, 5000, 10000
catalan1 = precalc(10, 1000)
catalan2 = precalc(10, 5000)
catalan3 = precalc(10, 10000)

def count_last_digit(catalan):
    count = {}
    for el in catalan:
        if el in count:
            count[el] += 1
        else:
            count[el] = 1

    for key in count:
        count[key] = count[key] / len(catalan)

    return count

count1 = count_last_digit(catalan1)
count2 = count_last_digit(catalan2)
count3 = count_last_digit(catalan3)

# print catalan 1 and catalan 2
def print_catalan(count):
    for key in count:
        print('The frequency of the last digit', key, 'is ', count[key])


-------- The test case with n = 1000 --------
The frequency of the last digit 1 is  0.002
The frequency of the last digit 2 is  0.056
The frequency of the last digit 5 is  0.004
The frequency of the last digit 4 is  0.073
The frequency of the last digit 9 is  0.003
The frequency of the last digit 0 is  0.781
The frequency of the last digit 6 is  0.03
The frequency of the last digit 8 is  0.05
The frequency of the last digit 7 is  0.001
-------- The test case with n = 5000 --------
The frequency of the last digit 1 is  0.0004
The frequency of the last digit 2 is  0.0292
The frequency of the last digit 5 is  0.0014
The frequency of the last digit 4 is  0.0414
The frequency of the last digit 9 is  0.0006
The frequency of the last digit 0 is  0.8692
The frequency of the last digit 6 is  0.0224
The frequency of the last digit 8 is  0.0352
The frequency of the last digit 7 is  0.0002
-------- The test case with n = 10000 --------
The frequency of the last digit 1 is  0.0002
The frequency of the last digit 2 is  0.0244
The frequency of the last digit 5 is  0.0008
The frequency of the last digit 4 is  0.0319
The frequency of the last digit 9 is  0.0003
The frequency of the last digit 0 is  0.9021
The frequency of the last digit 6 is  0.0162
The frequency of the last digit 8 is  0.024
The frequency of the last digit 7 is  0.0001

# We can also plot the bar chart to show it
x1 = list(count1.keys())
y1 = list(count1.values())
y2 = list(count2.values())
y3 = list(count3.values())
x = range(len(x1))

plt.figure(figsize=(13, 9))
# plot the bar separately
plt.bar(x1, y1, width=0.4, color='b', label='n = 1000')
plt.bar([i + 0.4 for i in x1], y2, width=0.4, color='r', label='n = 5000')
plt.bar([i + 0.8 for i in x1], y3, width=0.4, color='g', label='n = 10000')
plt.xlabel('Last digit of Catalan Number')
plt.ylabel('Frequency of the last digit')
plt.title('The frequency of the last digit of Catalan numbers')
plt.legend()

plt.show()

knitr::include_graphics('static/pic9.png')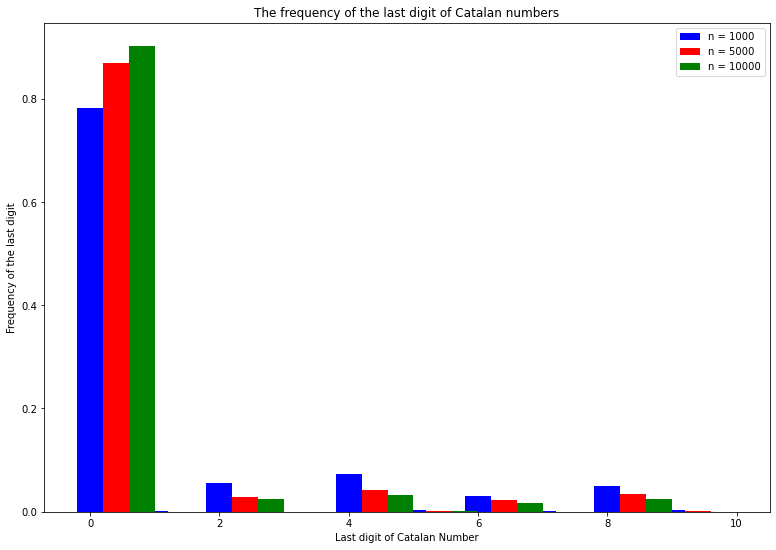

We test the case for $n = 1000$ , $n = 5000$ , and $n = 10000$ . From the bar chart and the output of our test, we may deduce from that in basis 10 the last digit of $c_{n}$ is never $3$ . When $n$ increase, we can find following - The probability for last digits of Catalan numbers is 0 getting increases. - The probability for last digits of Catalan numbers is even number getting decreases. - The probability for last digits of Catalan numbers is odd number (3 not included) is really small, which means the last digits of Catalan numbers is rarely odd when $n$ is a large number.

4.2 The length of large Catalan numbers

Definition 4.1
It can be proved (this is beyond the level of Bachelor 2, a possible reference is p.384 in Ph.Flajolet, R.Sedgewick, Analytic Combinatorics) that for every $n$ we have $\begin{matrix} ($) & \frac{4^{n}}{\sqrt{π n^{3}}} (1 - \frac{9}{8 n}) \leq c_{n} \leq \frac{4^{n}}{\sqrt{π n^{3}}}, \end{matrix}$ which yields very good approximations when $n$ is large. We will use this approximation to estimate the length (i.e. the number of digits) of $c_{n}$ when $n$ is a power of ten.

Consider the following table which records the length of $c_{10}$ , $c_{100}$ , $c_{1000}$ ,…

$c_{10^{n}}$	Number of digits of $c_{10^{n}}$
$c_{10}$	5
$c_{100}$	57
$c_{10^{3}}$	598
$c_{10^{4}}$	6015
$c_{10^{5}}$	60199
$c_{10^{6}}$	602051

(For instance, $c_{10} = 16796$ which has $5$ digits.)

The goal is to complete the table. (An interesting challenge could be to break the record of this sequence in the Online Encyclopedia of Integer Sequences!) For that purpose you have to

(Theory) Find somewhere (or reprove) the formula which gives the number of digits of a given integer.
Use this formula and python to complete the table. Warning: Do not try to explicitly compute $C a t_{10^{n}}$ since they grow too fast. Instead you need to figure out how to use equation ($) above.

For any positive integer $n$ , we assume the digits of $n$ is $i$ . We have the relation that $10^{i - 1} \leq n < 10^{i}$ Then we take the $\log_{10}$ for both side we have $i - 1 \leq \log (n) < i$ Then we can prove that the digits of any given number $n$ is $i = ⌊ \log (n) ⌋ + 1$

From the equation from Definition 4.1 and above we have $i = ⌊ \log (n) ⌋$ and $\frac{4^{n}}{\sqrt{π n^{3}}} (1 - \frac{9}{8 n}) \leq c_{n} \leq \frac{4^{n}}{\sqrt{π n^{3}}}$ . Then we take the $\log_{10}$ for both side we have $⌊ \log (\frac{4^{n}}{\sqrt{π n^{3}}} (1 - \frac{9}{8 n})) ⌋ + 1 \leq i = ⌊ \log (c_{n}) ⌋ \leq ⌊ \log (\frac{4^{n}}{\sqrt{π n^{3}}}) ⌋ + 1$ Since $n$ is a number of power 10, then we denote $n = 10^{k}$ where $k \geq 1$ and $k$ is an integer. Then we have $\begin{aligned} \log (\frac{4^{n}}{\sqrt{π n^{3}}} (1 - \frac{9}{8 n})) & = \log (\frac{4^{n}}{\sqrt{π n^{3}}}) + \log (1 - \frac{9}{8 n}) \\ = \log 4^{n} - (\frac{1}{2} \log (π) + \frac{3}{2} \log (n)) + \log (1 - \frac{9}{8 n}) \\ = 10^{k} \log 4 - (\frac{1}{2} \log (π) + \frac{3 k}{2}) + \log (1 - \frac{9}{8 n}) \end{aligned}$ Since $k \geq 1$ and $n = 10^{k}$ , then we know that $n$ goes really fast, therefore $\log (1 - \frac{9}{8 n})$ tend close to $0$ and we can neglect it. Then we have $i = ⌊ \log (\frac{4^{n}}{\sqrt{π n^{3}}} (1 - \frac{9}{8 n})) ⌋ + 1 = ⌊ 10^{k} \log 4 - (\frac{1}{2} \log (π) + \frac{3 k}{2}) ⌋ + 1$ Therefore, we can use the code below to complete the table.

# implement the formula above
def num_digits(n):
    ub = (10**n) * log10(4) - (1 / 2) * log10(pi) - (3 * n / 2) * log10(10)
    return math.floor(ub) + 1


for i in range(1, 20):
    print("The number of digits of Catalan, 10 **", i, "is", num_digits(i))\
    
The number of digits of Catalan, 10 ** 1 is 5
The number of digits of Catalan, 10 ** 2 is 57
The number of digits of Catalan, 10 ** 3 is 598
The number of digits of Catalan, 10 ** 4 is 6015
The number of digits of Catalan, 10 ** 5 is 60199
The number of digits of Catalan, 10 ** 6 is 602051
The number of digits of Catalan, 10 ** 7 is 6020590
The number of digits of Catalan, 10 ** 8 is 60205987
The number of digits of Catalan, 10 ** 9 is 602059978
The number of digits of Catalan, 10 ** 10 is 6020599899
The number of digits of Catalan, 10 ** 11 is 60205999117
The number of digits of Catalan, 10 ** 12 is 602059991310
The number of digits of Catalan, 10 ** 13 is 6020599913260
The number of digits of Catalan, 10 ** 14 is 60205999132775
The number of digits of Catalan, 10 ** 15 is 602059991327940
The number of digits of Catalan, 10 ** 16 is 6020599913279601

We can see from the result that ${C a t}_{10}$ grows really fast. The number of digits of ${C a t}_{10}$ is $5$ and the number of digits of ${C a t}_{10^{6}}$ is $602051$ . Therefore we use the formula gave above and simluated with the python code.

For larger and larger $n$ ’s the right column always begins with the same digits ( $60205...$ ) and explain this.

We have $i = ⌊ 10^{k} \log 4 - (\frac{1}{2} \log (π) + \frac{3 k}{2}) ⌋ + 1$ Since we want to prove that the right column always begins with the same digits ( $60205...$ ), then we can ignore the smaller part of $i$ , which means $(\frac{1}{2} \log (π) + \frac{3 k}{2})$ can be ignore since there are quite small compared to $10^{k} \log 4$ . Then compute $10^{k} \log 4$ with python code and we have for the value of $10^{k} \log (4)$ for $k \in [1, 20]$ . Since $\log (4) = 0.6020599913279624$ , so we consider the marginal case, when $k = 6$ , $10^{6} \log (4) = 602059.9913279624$ , and $\frac{1}{2} \log (π) + \frac{3 k}{2} < 9$ , therefore it would not influnce the second digits of $i$ . This also applys to the value of $i$ with bigger $k$ . Then we prove the theorem.

# return the number of 10^k log(4)
def num_digits2(n):
    ub = (10**n) * log10(4)
    return math.floor(ub)
  
print("--------- Question 5.2.3 ----------")
print('The value of log(4) is', log10(4))

--------- Question 5.2.3 ----------
The value of log(4) is 0.6020599913279624