Chapter 2 Computing Catalan Numbers

Definition 2.1 The Catalan numbers \(c_0,c_1,c_2,\dots\) are defined recursively as follows: \[\begin{align*} c_0&=1\\ c_1&=1\\ c_n&=\sum_{k=0}^{n-1} c_kc_{n-1-k}=c_0c_{n-1}+c_1c_{n-2}+\dots +c_{n-1}c_0 \qquad (\text{ for }n\geq 2). \tag{$\star$} \end{align*}\] For example, \[\begin{align*} c_2&=c_0c_1+c_1c_0=1\times 1+1\times 1=2,\\ c_3&=c_0c_2+c_1c_1+c_2c_0=1\times 2+1\times 1+2\times 1=5,\\ \dots \end{align*}\]

We write a recursive function CatalanRecursive(n) which returns the \(n\)-th Catalan number.

def CatalanRecursive(n):
    if n == 0:
        return 1
    if n == 1:
        return 1
    else:
        Cn = 0
        for i in range(0, n):
            Cn += CatalanRecursive(i) * CatalanRecursive(n - 1 - i)

    return Cn

We write a non-recursive function CatalanNotRecursive(n) which returns the \(n\)-th Catalan number.

def CatalanNonRecursive(n):
    if n == 0:
        return 1
    if n == 1:
        return 1
    C = [0] * (n + 1)
    C[0] = 1
    C[1] = 1
    for i in range(2, n + 1):
        C[i] = 0
        for j in range(0, i):
            C[i] += C[j] * C[i - j - 1]

    return C[n]

We can compare the execution times of these two method of computing the Catalan numbers, where we have the graph of following.

knitr::include_graphics('static/pic1.png')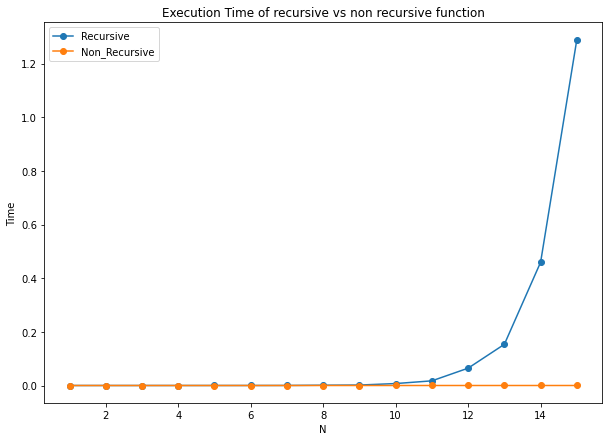

From the graph that we plot, we can see that the recursive function is much slower than the non recursive one. From \(n=10\) the recursive function takes much more time than the non recursive one and increases exponentially. This is due to in the computation of \(c_{n}\), the recursive function calls itself too much time with repeated computation. However, in the non recursive function we use list to store the values of \(c_{n}\) and we don’t need to compute them again.